Batas ng Ohm para sa isang magnetic circuit

Kung walang magnetic fluxes, malabong umiral ang modernong electrical engineering. Ang pagpapatakbo ng mga generator at de-koryenteng motor, mga electromagnet at mga transformer, mga instrumento sa pagsukat at mga sensor ng Hall ay batay sa paggamit ng magnetic field at mga katangian ng magnetic flux.

Upang tumutok at palakasin ang magnetic flux, ginagamit nila ang paggamit ng mga ferromagnetic na materyales. Ang mga ferromagnetic na materyales ay ginawa mga magnetic core — mga katawan ng mga kinakailangang hugis at sukat, mga core para sa pagdidirekta ng mga magnetic flux ng isa o ibang laki sa kinakailangang direksyon. Ang ganitong mga katawan, sa loob kung saan ang mga saradong linya ng magnetic induction ay pumasa, ay tinatawag na magnetic circuits.

Ginagawang posible ng mga kilalang katangian ng magnetic field na kalkulahin ang mga magnetic flux sa iba't ibang magnetic circuit. Ngunit para sa praktikal na gawain, mas maginhawang gumamit ng mga pangkalahatang kahihinatnan at mga batas ng magnetic circuit na nagmula sa mga batas ng magnetic field, sa halip na gamitin ang mga batas na ito nang direkta sa bawat oras. Ang paglalapat ng ilang mga patakaran sa mga magnetic circuit ay mas maginhawa para sa paglutas ng mga tipikal na praktikal na problema.

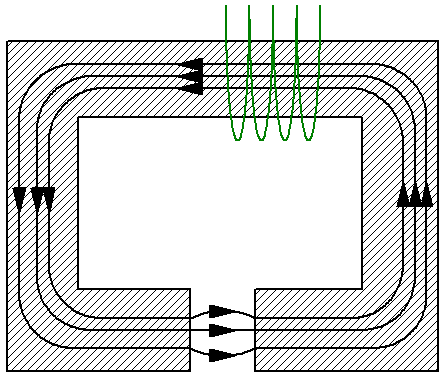
Halimbawa, isaalang-alang ang isang simpleng magnetic circuit na binubuo ng isang walang sanga na pamatok ng cross-section S, na kung saan ay gawa sa isang materyal na may pagkamatagusin mu… Ang pamatok ay may non-magnetic gap ng parehong lugar S, halimbawa hangin, at ang magnetic permeability sa gap — mu1 — ay iba sa magnetic permeability ng yoke. Dito maaari mong tingnan ang ibig sabihin ng linya ng induction at ilapat ang magnetic tension theorem dito:

Dahil ang mga linya ng magnetic induction ay tuloy-tuloy sa buong circuit, ang magnitude ng magnetic flux sa parehong yoke at ang gap ay pareho. Ngayon ginagamit namin ang mga formula para sa magnetic induction B at para sa magnetic flux F upang ipahayag ang lakas H ng magnetic field sa mga tuntunin ng magnetic flux F.

Ang susunod na hakbang ay upang palitan ang mga resultang expression sa itaas na formula ng magnetic flux theorem:

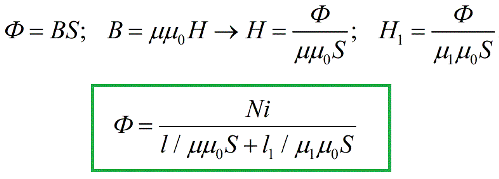
Nakakuha kami ng isang formula na halos kapareho ng kilala sa electrical engineering Batas ng Ohm para sa isang seksyon ng isang closed circuit, at ang papel ng EMF dito ay ginagampanan ng dami ng iN, na tinatawag na magnetomotive force (o MDF) ayon sa pagkakatulad sa electromotive force. Sa sistema ng SI, ang magnetomotive force ay sinusukat sa amperes.

Ang kabuuan sa denominator ay walang iba kundi isang pagkakatulad ng kabuuang paglaban ng kuryente para sa isang de-koryenteng circuit, at para sa isang magnetic circuit ito ay tinatawag na kabuuang magnetic resistance nang naaayon. Ang mga termino sa denominator ay ang mga magnetic resistance ng mga indibidwal na seksyon ng magnetic circuit.

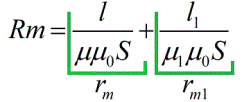
Ang mga magnetic resistance ay nakasalalay sa haba ng magnetic circuit, sa cross-sectional area nito, at sa magnetic permeability (katulad ng electrical conductivity para sa karaniwang batas ng Ohm).Bilang resulta, maaari mong isulat ang formula ng batas ng Ohm, para lamang sa isang magnetic circuit:

Iyon ay, ang pagbabalangkas ng batas ng Ohm na may kaugnayan sa isang magnetic circuit ay ganito ang tunog: «sa isang magnetic circuit na walang sumasanga, ang magnetic flux ay katumbas ng quotient ng dibisyon ng MDS sa pamamagitan ng kabuuang magnetic resistance ng circuit.»

Ito ay halata mula sa mga formula na ang magnetic resistance sa NE ay sinusukat sa weber amperes, at ang kabuuang magnetic resistance ng isang magnetic circuit ay numerong katumbas ng kabuuan ng magnetic resistances ng mga bahagi ng magnetic circuit na iyon.

Ang sitwasyong inilarawan ay wasto para sa isang walang sanga na magnetic circuit na kinabibilangan ng anumang bilang ng mga bahagi, sa kondisyon na ang magnetic flux ay sunud-sunod na tumagos sa lahat ng mga bahaging ito. Kung ang mga magnetic core ay konektado sa serye, kung gayon ang kabuuang magnetic resistance ay matatagpuan sa pamamagitan ng pagdaragdag ng mga magnetic resistance ng mga bahagi.

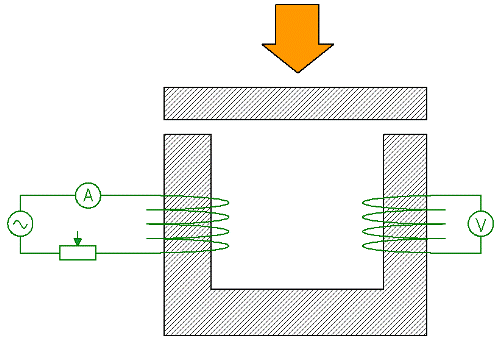
Isaalang-alang ngayon ang isang eksperimento na nagpapakita ng epekto ng pag-aatubili ng mga bahagi ng isang circuit sa kabuuang pag-aatubili ng isang circuit. Ang isang hugis-U na magnetic circuit ay na-magnetize ng coil 1, na pinapakain (alternating current) sa pamamagitan ng ammeter at rheostat. Ang isang EMF ay na-induce sa pangalawang winding 2, at ang mga pagbabasa ng voltmeter na konektado sa winding, tulad ng alam mo, ay proporsyonal sa magnetic flux sa magnetic circuit.

Kung pinapanatili mo ngayon ang kasalukuyang sa pangunahing paikot-ikot na hindi nagbabago sa pamamagitan ng pag-regulate nito gamit ang isang rheostat, at sa parehong oras pindutin ang bakal na plato laban sa magnetic circuit sa itaas, pagkatapos ng kabuuang magnetic resistance ng circuit ay lubos na mababawasan, ang pagbabasa ng tataas ang voltmeter nang naaayon.

Siyempre, ang mga termino sa itaas, tulad ng "magnetoresistance" at "magnetomotive force", ay mga pormal na konsepto, dahil wala sa magnetic flux na gumagalaw, walang mga gumagalaw na particle, ito ay isang visual na representasyon lamang (tulad ng isang fluid flow model) ng mas malinaw na pag-unawa sa mga batas...

Ang pisikal na kahulugan ng eksperimento sa itaas at iba pang katulad na mga eksperimento ay upang maunawaan kung paano ang pagpapakilala ng mga di-magnetic na gaps at magnetic na materyales sa magnetic circuit ay nakakaapekto sa magnetic flux sa magnetic circuit.

Sa pamamagitan ng pagpapakilala, halimbawa, ng isang magnet sa isang magnetic circuit, nagdaragdag kami ng karagdagang mga molekular na alon sa mga katawan na nakapaloob na sa circuit, na nagpapakilala ng mga karagdagang magnetic flux. Ang mga pormal na konsepto tulad ng "magnetic resistance" at "magnetomotive force" ay nagpapatunay na napaka-maginhawa kapag nilutas ang isang praktikal na problema, kaya naman matagumpay itong ginagamit sa electrical engineering.