Mga halaga ng RMS ng kasalukuyang at boltahe

Ang alternating sinusoidal current ay may iba't ibang instant na halaga sa panahon. Ito ay natural na magtanong, anong halaga ng kasalukuyang ang susukatin kasama ang ammeter na kasama sa circuit?

Kapag kinakalkula ang mga alternating current circuit, pati na rin ang mga pagsukat ng elektrikal, hindi maginhawang gumamit ng madalian o amplitude na mga halaga ng mga alon at boltahe, at ang kanilang mga average na halaga sa isang panahon ay zero. Bilang karagdagan, ang elektrikal na epekto ng isang pana-panahong pagbabago ng kasalukuyang (ang dami ng init na inilabas, ang perpektong operasyon, atbp.) ay hindi matantya ng amplitude ng kasalukuyang ito.

Ang pinaka-maginhawa ay ang pagpapakilala ng mga konsepto ng tinatawag na epektibong mga halaga ng kasalukuyang at boltahe... Ang mga konsepto na ito ay batay sa thermal (o mekanikal) na pagkilos ng kasalukuyang, na hindi nakasalalay sa direksyon nito.

Root mean square value ng alternating current - ito ang halaga ng direktang kasalukuyang kung saan sa panahon ng alternating current ang parehong halaga ng init ay inilabas sa konduktor tulad ng sa panahon ng alternating current.

Upang suriin ang mga aksyon na ginawa alternating current, ihahambing namin ang mga aksyon nito sa thermal effect ng direktang kasalukuyang.

DC power P A na dumadaan sa resistance r ay magiging P = P2r.

Ang AC power ay ipinahayag bilang ang average na epekto ng instantaneous power Az2r sa buong panahon o ang average ng (I am x sinωT)2 NS r para sa parehong oras.

Hayaan ang average na halaga ng t2 para sa panahon ay M. Equating ang kapangyarihan ng direktang kasalukuyang at kapangyarihan ng alternating kasalukuyang, mayroon kaming: Az2r = Mr -n, kung saan Az = √M,

Ang dami I ay tinatawag na epektibong halaga ng alternating current.

Ang average na halaga ng i2 sa alternating current ay tinutukoy bilang mga sumusunod.

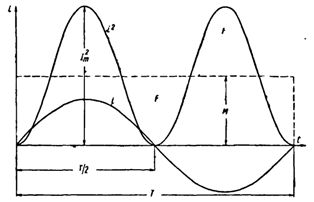
Bumuo tayo ng sinusoidal current curve. Sa pamamagitan ng pag-squaring sa bawat instant na kasalukuyang halaga, nakakakuha tayo ng P versus time curve.

Halaga ng AC rms

Ang parehong mga kalahati ng curve na ito ay nasa itaas ng pahalang na axis, dahil ang mga negatibong alon (-i) sa ikalawang kalahati ng panahon, kapag naka-squad, ay nagbibigay ng mga positibong halaga.

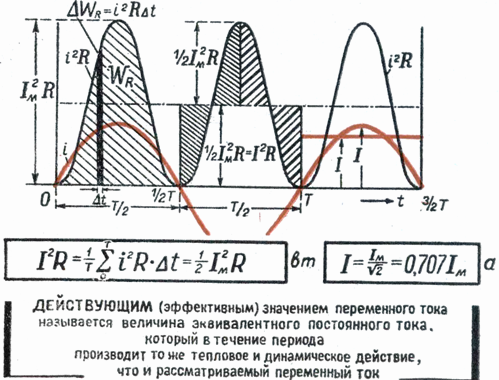
Bumuo ng isang parihaba na may base T at lugar na katumbas ng lugar na hangganan ng curve i2 at horizontal axis. Ang taas ng rectangle M ay tumutugma sa average na halaga ng P para sa panahon. Ang halaga ng panahon na ito, na kinakalkula gamit ang mas mataas na matematika, ay magiging katumbas ng 1/2 I2m... Samakatuwid, M. = 1/2 I2m

Dahil ang rms value na Im alternating current ay Im = √Mthen finally I = Im / √2

Katulad nito, ang ugnayan sa pagitan ng rms at mga halaga ng amplitude para sa boltahe U at E ay may anyo:

U = Um / √2E = Em / √2

Ang mga epektibong halaga ng mga variable ay ipinahiwatig ng malalaking titik na walang mga subscript (I, U, E).

Batay sa itaas, maaari nating sabihin na ang epektibong halaga ng isang alternating current ay katumbas ng tulad ng isang direktang kasalukuyang, na, na dumadaan sa parehong paglaban ng alternating current, ay naglalabas ng parehong dami ng enerhiya sa parehong oras.

Ang mga instrumento sa pagsukat ng elektrikal (ammeters, voltmeters) na kasama sa isang alternating current circuit ay nagpapahiwatig ng mga epektibong halaga ng kasalukuyang o boltahe.

Kapag gumagawa ng mga diagram ng vector, mas maginhawang ipagpaliban hindi ang amplitude, ngunit ang mga epektibong halaga ng mga vector. Para dito, ang mga haba ng mga vector ay binabawasan ng √2 isang beses. Hindi nito binabago ang lokasyon ng mga vector sa diagram.