Mga electric circuit na may non-sinusoidal current

Non-sinusoidal currents at ang kanilang pagkabulok

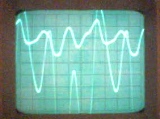Sa isang de-koryenteng circuit, ang mga non-sinusoidal na alon ay maaaring mangyari sa dalawang dahilan:

1. ang electric circuit mismo ay linear, ngunit ang isang non-sinusoidal na boltahe ay kumikilos sa circuit,

2. ang boltahe na kumikilos sa circuit ay sinusoidal, ngunit ang electrical circuit ay naglalaman ng mga non-linear na elemento.

Maaaring may parehong dahilan. Ang kabanatang ito ay tumatalakay sa mga circuit para sa unang punto lamang. Sa kasong ito, ang mga non-sinusoidal na boltahe ay itinuturing na pana-panahon.

Ang mga generator ng periodic pulse ay ginagamit sa iba't ibang mga aparato ng radio engineering, automation, telemechanics. Ang hugis ng mga pulso ay maaaring magkakaiba: saw, stepped, rectangular (Fig. 1).

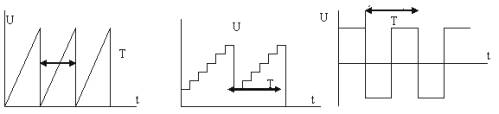
Larawan 1. Mga hugis ng pulso

Ang mga phenomena na nagaganap sa isang linear electrical circuit sa ilalim ng periodic ngunit non-sinusoidal voltages ay pinakamadaling pag-aralan kung ang curve ng boltahe ay pinalawak sa isang trigonometric Fourier series:

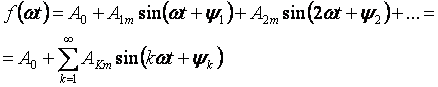
Ang unang termino ng seryeng A0 ay tinatawag na constant component o zeroth harmonic, ang pangalawang termino ng serye

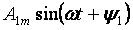
— ang pangunahing o unang harmonic at lahat ng iba pang mga miyembro ng form

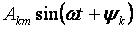
para sa k> 1 ay tinatawag na mas mataas na harmonika.

Kung sa expression (3.1) binuksan natin ang sine ng kabuuan, maaari tayong lumipat sa isa pang anyo ng pagsulat ng serye:

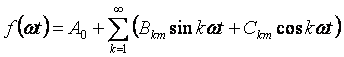Kung ang function ay simetriko tungkol sa abscissa axis, kung gayon ang serye ay hindi naglalaman ng isang pare-parehong bahagi. Kung ang function ay simetriko tungkol sa ordinate axis, kung gayon ang serye ay walang mga sine. Ang function ay simetriko tungkol sa pinagmulan at walang mga cosine.

Ang ilang mga halimbawa ng pagpapalawak ng serye ay ibinigay sa isang talahanayan. 1 at makukuha rin ang mga ito sa sangguniang literatura.

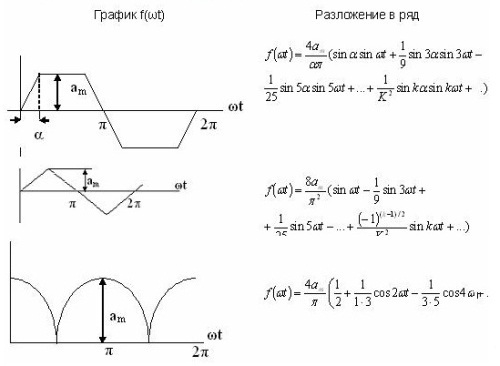
Talahanayan 1. Pagpapalawak ng serye ng Fourier

Pagkalkula ng mga non-sinusoidal current circuits

Ang circuit ay kinakalkula para sa bawat harmonic ayon sa modelo. Ang circuit ay kinakalkula nang maraming beses hangga't may mga harmonika sa boltahe na kumikilos sa circuit. Sa kasong ito, kinakailangang isaalang-alang ang isang bilang ng mga katangian.

Dapat tandaan na ang paglaban ng inductive element ay tumataas habang tumataas ang harmonic number

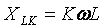
at ang capacitive element, sa kabaligtaran, ay bumababa:

Dapat din itong isaalang-alang na ang pare-parehong bahagi ng kasalukuyang ay hindi dumadaan sa kapasitor at ang inductance ay hindi isang pagtutol dito.

Bilang karagdagan, hindi dapat kalimutan ng isa ang posibleng mga phenomena ng resonance hindi lamang sa pangunahing harmonic, kundi pati na rin sa mas mataas na harmonic.

Mga diagram ng vector maaaring i-plot para sa bawat harmonic nang hiwalay.

Ayon sa prinsipyo ng superposisyon, ang kasalukuyang ng bawat sangay ay maaaring binubuo ng kabuuan ng mga indibidwal na termino (zero, pangunahing at mas mataas na harmonika):

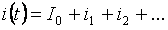
Ang halaga ng rms ng kabuuang kasalukuyang sangay ay maaaring matukoy ng average na halaga ng mga indibidwal na harmonic na alon:

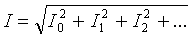
Ang aktibong kapangyarihan ng di-sinusoidal na kasalukuyang ay katumbas ng kabuuan ng mga aktibong kapangyarihan ng mga indibidwal na harmonika:

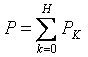
Nasa ibaba ang isang pangkalahatang halimbawa para sa pagkalkula ng mga non-sinusoidal current circuit. Ang lahat ng mga alon, boltahe, resistensya ay magkakaroon ng dalawang indeks: ang unang digit ay nangangahulugang ang numero ng sangay at ang pangalawang digit ay ang maharmonya na numero. Input na boltahe:

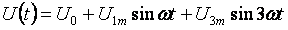
• Permanenteng sangkap

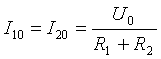
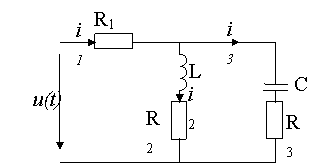
Figure 2. Electrical diagram

• Major Harmonic:

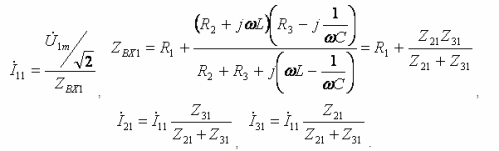
• Ikatlong harmonic:

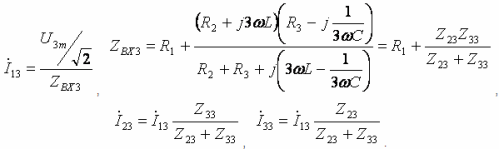
Basahin din: Ang pinakakaraniwang AC to DC rectification scheme