Thomson effect — isang thermoelectric phenomenon

Kapag ang isang direktang kuryente ay dumaan sa isang kawad, ang kawad na iyon ay pinainit ayon sa sa batas ng Joule-Lenz: ang inilabas na thermal power sa bawat unit volume ng conductor ay katumbas ng produkto ng kasalukuyang density at ang lakas ng electric field na kumikilos sa conductor.

Ito ay dahil ang mga gumagalaw sa wire sa ilalim ng pagkilos ng isang electric field libreng elektron, na bumubuo ng isang kasalukuyang, bumangga sa mga node ng kristal na sala-sala sa daan at ilipat ang bahagi ng kanilang kinetic na enerhiya sa kanila, bilang isang resulta, ang mga node ng kristal na sala-sala ay nagsisimulang mag-vibrate nang mas malakas, iyon ay, ang temperatura ng konduktor tumataas sa kabuuan nito.

Ang higit pa lakas ng electric field sa isang wire — mas mataas ang bilis ng mga libreng electron ay may oras upang mapabilis bago sila bumangga sa mga node ng crystal lattice, mas maraming kinetic energy ang mayroon sila ng oras upang makuha sa libreng landas at mas maraming momentum ang kanilang inilipat sa mga node ng ang kristal na sala-sala sa sandaling ito sa isang banggaan sa kanila.Ito ay malinaw na ang mas malaki ang electric field, ang mga libreng electron sa konduktor ay pinabilis, mas init ang inilabas sa dami ng konduktor.

Ngayon isipin natin na ang wire sa isang gilid ay pinainit. Iyon ay, ang isang dulo ay may temperatura na mas mataas kaysa sa kabilang dulo, habang ang kabilang dulo ay may humigit-kumulang kapareho ng temperatura ng nakapalibot na hangin. Nangangahulugan ito na sa pinainit na bahagi ng konduktor ang mga libreng electron ay may mas mataas na bilis ng thermal movement kaysa sa kabilang bahagi.

Kung iiwan mo ngayon ang wire, unti-unti itong lalamig. Ang ilan sa init ay direktang ililipat sa nakapaligid na hangin, ang ilan sa init ay ililipat sa hindi gaanong init na bahagi ng kawad, at mula dito sa nakapaligid na hangin.

Sa kasong ito, ang mga libreng electron na may mas mataas na mga rate ng thermal movement ay maglilipat ng momentum sa mga libreng electron sa hindi gaanong pinainit na bahagi ng konduktor hanggang sa ang temperatura sa buong volume ng konduktor ay equalize, iyon ay, hanggang sa mga rate ng thermal. Ang paggalaw ng mga libreng electron sa buong dami ng konduktor ay equalized.

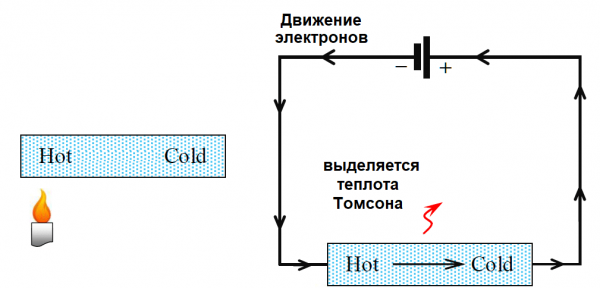
Gawin nating kumplikado ang eksperimento. Ikinonekta namin ang wire sa isang direktang kasalukuyang pinagmumulan, na pinainit ang gilid ng apoy kung saan ang negatibong terminal ng pinagmulan ay ikokonekta. Sa ilalim ng impluwensya ng electric field na nilikha ng pinagmulan, ang mga libreng electron sa wire ay magsisimulang lumipat mula sa negatibong terminal patungo sa positibong terminal.

Bilang karagdagan, ang pagkakaiba sa temperatura na nilikha sa pamamagitan ng preheating ng wire ay makakatulong sa paggalaw ng mga electron na ito mula sa minus hanggang plus.

Masasabi nating ang electric field ng source ay nakakatulong sa pagkalat ng init sa kahabaan ng wire, ngunit ang mga libreng electron na gumagalaw mula sa mainit na dulo hanggang sa malamig na dulo ay kadalasang pinabagal, na nangangahulugang naglilipat sila ng karagdagang enerhiya ng init sa mga nakapaligid na atomo.

Iyon ay, sa direksyon ng mga atomo na nakapalibot sa mga libreng electron, ang karagdagang init ay inilabas na may kaugnayan sa init ng Joule-Lenz.

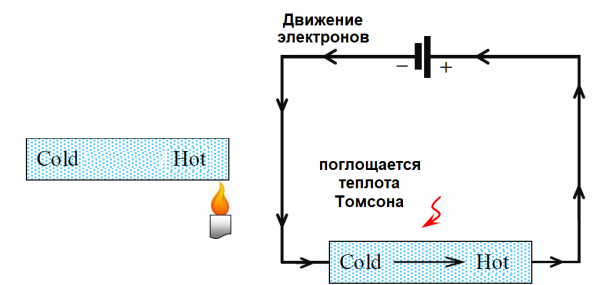
Ngayon painitin muli ang isang bahagi ng wire gamit ang apoy, ngunit ikonekta ang kasalukuyang pinagmumulan ng positibong lead sa pinainit na bahagi. Sa gilid ng negatibong terminal, ang mga libreng electron sa konduktor ay may mas mababang bilis ng thermal movement, ngunit sa ilalim ng pagkilos ng electric field ng pinagmulan ay nagmamadali sila sa pinainit na dulo.

Ang thermal motion ng mga libreng electron na nilikha sa pamamagitan ng preheating ng wire ay nagpapalaganap sa paggalaw ng mga electron na ito mula minus hanggang plus. Ang mga libreng electron na lumilipat mula sa malamig na dulo hanggang sa mainit na dulo ay karaniwang pinabilis sa pamamagitan ng pagsipsip ng enerhiya ng init mula sa pinainit na kawad, ibig sabihin ay sinisipsip nila ang enerhiya ng init ng mga atomo na nakapalibot sa mga libreng electron.

Natagpuan ang epektong ito noong 1856 British physicist William Thomsonna natagpuan iyon sa isang hindi pare-parehong pinainit na direktang kasalukuyang konduktor, bilang karagdagan sa init na inilabas alinsunod sa batas ng Joule-Lenz, ang karagdagang init ay ilalabas o maa-absorb sa dami ng konduktor, depende sa direksyon ng kasalukuyang (ikatlong thermoelectric effect) .

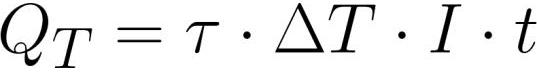
Ang halaga ng init ng Thomson ay proporsyonal sa magnitude ng kasalukuyang, ang tagal ng kasalukuyang, at ang pagkakaiba ng temperatura sa konduktor.t — Thomson coefficient, na kung saan ay ipinahayag sa volts bawat kelvin at may parehong laki bilang thermoelectromotive na puwersa.

Iba pang mga epekto ng thermoelectric: Seebeck at Peltier effect